経理側から機械学習を使ってみる
自分は長く経理をやっていて、学生、社会人と、数学・統計・プログラムの素養はありません。『できたらいいこと』については経理実務の経験からそれなりにあるのですが、『仕組み』の部分は見様見真似でトライアンドエラーです。
『文系経理が機械学習を触ってできたこと』を記事にしていきたいと思います。
データサイエンス側の人には、技術的な部分はスルーしてもらって、経理側のニーズを参考にしてください。
経理側の人には、自分のスキルを広げる分野として、機械学習ありかも?と思ってもらえたらうれしいです。どんな業務に使えるのか参考にしてください。
経理で使う最初の機械学習は決定木がおすすめ
経理で使う機械学習というと、よくみるのが異常値検出です。
いかにも機械学習らしい用途ですが、実効性のある仕組みにするのはかなり難しいと思います。また、大量のデータから学習する手法より、まずは明確にプログラムした手法で異常値検出をしっかりやる方が先です。人間が目でチェックしている内容をプログラム(エクセルでも十分です)に置き換え、漏れなく正確にチェックする仕組みを作ることをまずやりましょう。自分も含めて、この部分がしっかりできていない経理は多いのではないでしょうか?いずれ記事にしていきたいと思っています。
文系経理が最初に取り組む機械学習としては、もっと簡単でわかりやすいものがいいと思いますので、最初は決定木による業績分析がおすすめです。
ということなんですが、正直に言います。自分でやってみて、どうも効果的な分析にならなかったので、実際には社内での業績説明に資料としてまだ使っていません。反省を込めてどうやったのかまとめました。いずれ再チャレンジしてみます。
Pythonでやっています
Pythonは、Anacondaをインストールしています。
ここではAnacondaのインストールはとりあげません。
ググるといっぱいでてきますのでどれかを参考にインストールしてください。
決定木は広く使われているらしい?
機械学習に決定木というものがあります。
AIはよくブラックボックスで中のロジックがわからないといわれることが多いですが、決定木はホワイトボックスといわれていて、ロジックがシンプルで非常に明快で人間にも理解できます。
(計算の仕組みは後半にある『決定木の仕組み』を読んで例題を解いてみてください。手を動かして計算すると頭に入ると思います)
機械学習の手法の中では、決定木は一般に広く使用されている手法らしく、マーケティングや経営分析などで活用されています、と、ググると書いてあるサイトが多いですが、本当でしょうか?
実際に世の中でどのくらい使われているのかはよくわかりません。少なくとも、自分の会社ではまったく使われていません。(笑)
MACROMILLでは決定木によるデータ分析・解析のサービスがあるようです。
サービス一覧 データ分析・解析
決定木でできること
データを分類したいとします。データの列は、分類データ(目的変数)が一列、あとは分類と関係ありそうなデータ(説明変数)を何列か並べます。このデータを決定木で分析すると、分類のキーになりそうな説明変数の閾値を探し、枝分かれの木のような図で目的変数を区分してくれます。
例えば、複数の店舗がX,Yの地区にわかれ、商品A-Dを扱っているとします。この表のデータを、利益率の高さ・低さを目的変数としてPythonで処理すると、地区や商品ごとの売上で分類し、決定木として図が作成されます。
| 店舗 | 利益率 | 地区 | 商品A売上 | 商品B売上 | 商品C売上 | 商品D売上 |
| 1 | 高 | X地区 | 50 | 45 | 50 | 40 |
| 2 | 低 | X地区 | 45 | 35 | 20 | 35 |
| 3 | 低 | X地区 | 20 | 35 | 40 | 85 |
| 4 | 高 | Y地区 | 30 | 30 | 45 | 50 |
| 5 | 低 | X地区 | 45 | 30 | 30 | 110 |
| 6 | 高 | X地区 | 40 | 35 | 45 | 70 |
| 7 | 高 | Y地区 | 30 | 50 | 25 | 35 |
| 8 | 低 | Y地区 | 35 | 45 | 30 | 60 |
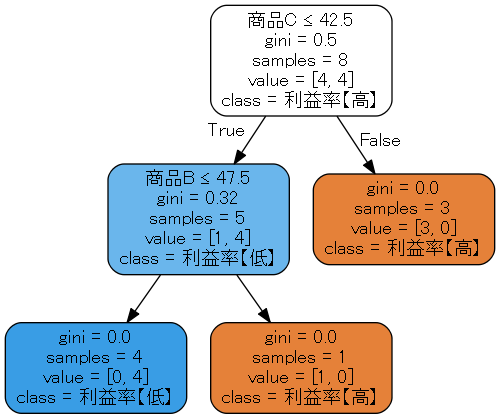
商品Cの売上が42.5以上ある店舗(8店舗のうち3店舗)はすべて利益率が高い。
注:商品C≦42.5⇒False(売上が42.5以下がFalse=以上)。店舗数はsamples
商品Cの売上が42.5未満の店舗のうち、商品Bの売上が47.5以上の店舗(1店舗)は利益率が高い。
これで商品C,Bの閾値のみで利益率の高い店舗(8店舗中4店舗)と低い店舗がすべて区分されました。
地区も商品A,Dも影響はあるのでしょうが、商品Cの売上と商品Bの売上だけで分類すると、儲かっているところと儲かっていないところがすっきり区分されました。
さて、この決定木を見せて、『利益の決め手は商品CとBの売上です!』と説明して大丈夫でしょうか?
さすがにそれは実務ではまずいと思います。あくまで計算でわけているだけなので、定性的情報による分析は人が行う必要があります。例外的な部分の特殊要因を説明しつつ、一般的な傾向分析の補強資料として『場合により』有効だと思います。
しかし、数字をちょっと入れ替えて返ってくる決定木を眺めていると、ちょっとどうかな?という場合も多いです。みなさんも試してください。(Pythonのコードは最後に参照サイトを示しています)
試行錯誤の業績分析
決定木を使用して、業績分析が効果的にできないか、試してみました。
うちの会社で、利益が高い営業所と低い営業所(目的変数。営業所の数は約20)を、4つのサービス(説明変数)で同様の分析をやってみました。商品であれば原価は割と共通部分が多いかもしれませんが、当社のサービスは原価が営業所ごとで結構違うので、斬新な視点で資料が作れるのでは?と期待しました。
しかし、いくつかの月次データで分類してみましたが、うまく分類されても、じっくりみればわかるじゃん?という感じです。いくつかの分岐でうまく分類されないのでその理由を考えていくと、そもそもやらなくていいか、という感じになってきます。
役に立つ感じにならないのはなぜか考えてみました。やはり、20営業所くらいだと、しばらく経理にいれば、個別の特徴が頭に入り、さまざまな数値以外の情報と一緒に1営業所ごとにじっくり見れるので、いくつかの数値だけで計算した区分では役に立つ情報が生み出せません。
役に立つ情報にするにはどうしたらいいのか考えてみました。
・普段考えない絶妙な目的変数を設定し、普段見ない数値を説明変数にする
・全体をしっかり把握できない数(100以上?)のものを対象にする
・状況がどんどん変わるものを対象にする
・新しく着任した場合等、個別の特徴が頭に入っていない最初だけ使う
個別の特徴が割と変わらず、頭に入る程度の数だと不要かもしれません。
また、馴染みのない図なので、説明を受ける経営層から拒否反応が出るかもしれないという、そもそも的な問題もあります。しかし、いずれリベンジして業績分析の方法を変えていきたいです!
決定木の仕組み
Pythonのライブラリで決定木を使用すると、アルゴリズムはcartになります。
ジニ不純度
あるノードで、アイテムがいくつかのクラスに分類されます。(ノード番号\(t\)、アイテム数\(n\)、クラス数\(c\))
クラス\(i\)に属するアイテム数を\(n_i\)とすると、ノード\(t\)での割合\(p(i|t)\)は、
\(p(i|t)=\frac{n_i}{n}\)
となります。このとき、ジニ不純度\(I_G(t)\)を次のとおり定義します。
\(I_G(t)=1 – \sum_{i=1}^{c}p(i|t)^2\)
不純度が低い組み合わせとなるように、特徴量で分岐をつくるのがCARTです。
例題1
次のジニ不純度を求めましょう。
リンゴが3つだけのノード
リンゴが3つ、みかんが3つのノード
リンゴが2つ、みかんが2つ、イチゴが2つのノード
利得(Gain)の計算
\(\Delta I_G(t)=I_G(t_B) – w_LI_G(t_L) – w_RI_G(t_R)\)
\(t_B\) :分岐前のノード
\(t_L,t_R\) :分岐後の左ノード・右ノード
\(w_L,w_R\) :分岐後のノードの重み(分岐前に対するデータ量の割合)
分岐したときに、不純度が低くなるほど、値は大きくなります。 すべての組み合わせを計算し、Gainが最も大きい組み合わせで分岐をつくります。
重要度(importance)
CARTでは、ジニ不純度が最小になるように、「特徴量」を使って分岐させます。
ある特徴量に関し、分岐に使われたすべてのノードにおける、分岐前と分岐後のジニ不純度の差を合計したものを、 その特徴量の「重要度」といいます。(減少させたジニ不純度の合計)
ある特徴量\(j\)が分割対象となるノード\(i\)のノード数を\(n\)とすると、重要度\(I(j)\)は以下で定義されます。
\(I(j)=\sum_{i=1}^{n}(N(i)\times G(i) – N_{left_child}(i)\times G_{left_child}(i)\)
\(- N_{right_child}(i)\times G_{right_child}(i))\)
ノード\(i\)のアイテム数は\(N\)、ジニ不純度は\(G\)です。
例題2
「決定木でできること」の数値で重要度を計算してみましょう。(足すと1になるように正規化します)
例題の答え
例題1の答え
リンゴが3つだけのノード
\(1-(1^2)=0\)
リンゴが3つ、みかんが3つのノード
\(1-(\frac{1}{2}^2 + \frac{1}{2}^2)=\frac{1}{2}\)
リンゴが2つ、みかんが2つ、イチゴが2つのノード
\(1-(\frac{1}{3}^2 + \frac{1}{3}^2 + \frac{1}{3}^2)=\frac{2}{3}\)
混在するほどジニ不純度が高くなっていくのが感じられたでしょうか?
例題2の答え
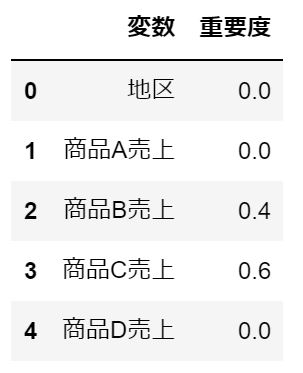
\( I(\) 商品C \()= 8\times 0.5 – 5\times 0.32 – 3\times 0.0 = 2.4\)
\( I(\) 商品B \()= 5\times 0.32 – 4\times 0.0 – 1\times 0.0 = 1.6\)
商品C \( :2.4\div 4=0.6\)
商品B \( :1.6\div 4=0.4\)
仕組みの説明と演習問題はGitHubにもおいています。参考にしてください。
*『DecisionTree.ipynb』ファイルにまとめていますが、Jupiter Notebookが動く環境でないとみれません。



